단층 퍼셉트론으로 AND, OR 게이트를 표현할 수 있고, 다층 퍼셉트론을 통해 XOR게이트를 표현할 수 있다는 것을 알았다.
이번에는 신경망과 퍼셉트론의 차이점인 활성화 함수에 대해서 다뤄본다.
1. 신경망과 퍼셉트론
신경망은 입력층(0층) > 은닉층 > 출력층으로 나눌 수 있다.
신경망과 퍼셉트론의 차이점을 이해하기 위해, 퍼셉트론을 다시 생각해본다.

$ y = \begin{Bmatrix}
0 (b + w_{1}x_{1}+ w_{2}x_2 \leq \theta ) \\
1 (b + w_{1}x_{1}+ w_{2}x_2 > \theta \end{Bmatrix} $
이 식을 조금 다른 형태로 작성해본다면,
$ y = h(b + w_{1}x_{1}+ w_{2}x_2) $
$ h(x) = \begin{Bmatrix}
0 (x \leq 0) \\
1 (x > 0 )
\end{Bmatrix} $
입력신호의 총합이 h(x) 함수를 거쳐 변환되어 출력되는 과정을 따로 표현한 것이다.
즉, h(x) 함수는 입력신호를 출력 신호로 변환하는 함수인 것이다.
이것을 활성화 함수라고 부른다.
2. 활성화 함수 - 계단, 시그모이드, ReLU
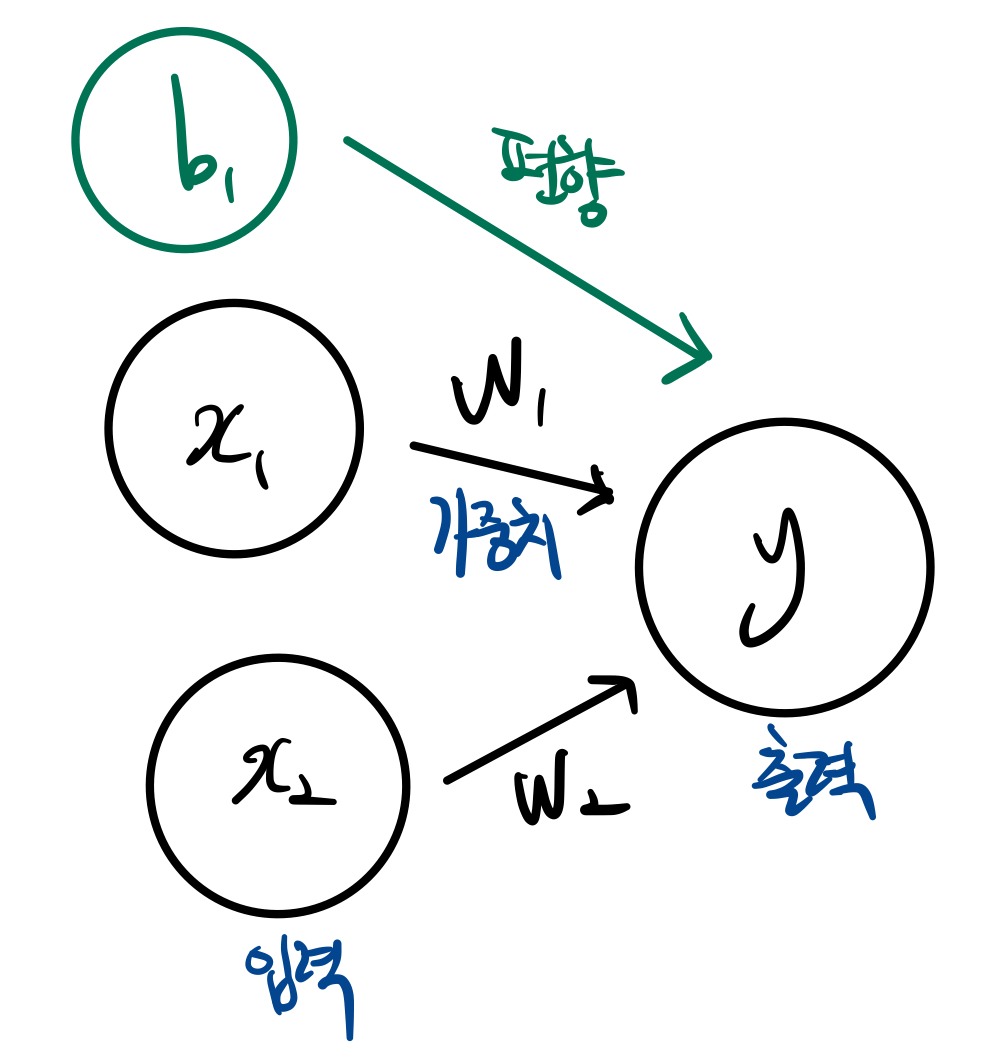

가중치 신호를 조합한 결과가 a 라는 노드가 되는 것이고, 활성화 함수 h(x) 를 통과해서 y라는 노드로 변환된다.
퍼셉트론의 활성화함수는?
특정 임계값을 경계로 출력이 바뀌는 계단함수가 활성화 함수이다.
계단 함수는 0을 경계로 출력이 0에서 1로 바뀐다.

import numpy as np
import matplotlib.pyplot as plt
def step_function(x):
return np.array(x > 0, dtype=int)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.title('step')
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
신경망에서 이용하는 활성화 함수
1. 시그모이드 함수 sigmoid function
$ h(x) = 1 / 1 + exp(-x) $
$ exp(-x) $ 는 $ e^{-x} $ 를 뜻하며, $ e $ 는 자연상수 2.178.. 이다.

퍼셉트론(계단함수)에서는 뉴런 사이에 0과 1이 흐르지만, 신경망(시그모이드) 에서는 연속적인 실수가 흐른다.
두 함수의 공통점이라면, 비선형 함수이다.
비선형 함수를 사용해야 하는 이유
신경망에서는 비선형 함수를 사용한다.
선형 함수를 사용하면, 신경망의 층을 깊게 하는 의미가 없어지기 때문이다.
선형함수는 층을 깊게 해도, 은닉층이 없는 함수로 구현이 가능하다.
즉, $ h(x) = cx $라는 활성화 함수가 있다고 가정하자.
를, 층을 3개로 넣어서 $ y(x) = h(h(h(x)) $ 로 표현한다면,
결국 $ y(x) = c*c*c*x $, $ y(x) = c^{3}x $,
결국 $ a = c*3 $ 일 때, 에 $ h(x) = cx $ 와 $ y(x)=ax $ 는 차이가 없다.
따라서, 은닉층을 구성하고 싶다면 활성화 함수로는 반드시 비선형 함수를 사용해야 한다.
2. ReLU
시그모이드 함수 외에, 많이 사용하고 있는 함수는 ReLU 함수이다.
입력이 0을 넘으면 입력을 그대로 출력하고, 0 이하면 0을 출력하는 함수이다.
$ h(x) = \begin{Bmatrix}
0 (x \leq 0) \\
x (x > 0 )
\end{Bmatrix} $

import matplotlib.pyplot as plt
def relu(x):
return np.maximum(0,x)
x = np.arange(-5.0,5.0,0.1)
y = relu(x)
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.title('relu')
plt.show()
'Python > Algorithm' 카테고리의 다른 글
| Linear Algebra for AI_1 (0) | 2025.02.23 |
|---|---|
| 항등 함수와 소프트맥스 함수 (0) | 2024.09.23 |
| 퍼셉트론과 논리회로 1 (1) | 2024.09.18 |
| [Algorithm] 자료구조와 알고리즘 - 3. 자료구조 - 스택(Stack) (0) | 2023.09.07 |
| [Algorithm] 자료구조와 알고리즘 - 2. 자료구조 - 큐(Queue) (0) | 2023.09.06 |


