KNN 알고리즘
KNN(최근접 이웃) 알고리즘은 지도 학습 알고리즘으로, 가장 가까운 이웃들의 정보를 사용하여 새로운 데이터 포인트를 분류 또는 회귀하는 알고리즘이다. (개념에 대한 설명은 아래 포스팅을 참고)
https://datapilots.tistory.com/101
[ML]K-NN 알고리즘
K-Nearest Neighbor : KNN , 최근접 이웃 개요 휘귀와 분류 모두 가능한 Memory-Based Learning 지도학습 알고리즘이다. (분류에 더 많이 사용) 이 알고리즘은, 유사한 데이터 포인트는 유사한 레이블이나 값을
datapilots.tistory.com
KNN 알고리즘 모델 피팅
데이터 형식
x : 행렬(metrix)
y : 벡터(vector)
간단한 알고리즘 피팅 해보자.
x1 = np.arange(2, 21, 2) # 2부터 20까지의 숫자를 가지는 배열 생성
x1array([ 6, 12, 18, 24, 30, 36, 42, 48, 54, 60])
배열을 생성한다. 그리고 해당 배열을 행렬 형태로 바꿔주고 x 변수로 만들어준다.
x = x1.reshape(-1, 1)
xarray([[ 2],
[ 4],
[ 6],
[ 8],
[10],
[12],
[14],
[16],
[18],
[20]])
y 변수를 입력한다.
y = np.arange(2, 21, 2) * 3
y
🔎 학습
knn_re=KNeighborsRegressor(n_neighbors=2).fit(x,y)
🔎 예측
print(knn_re.predict([[5]]))#비슷하게 예측
print(knn_re.predict([[20]]))#Knn 한계 예시
print(knn_re.predict([[30]]))#Knn 한계 예시
print(knn_re.predict([[40]]))#Knn 한계 예시[12.5]
[47.5]
[47.5]
[47.5]
예측값을 확인해 봤을 때, 학습한 x 값의 범위를 벗어나게 되면, 학습한 범위 내 가장 큰 값의 y를 반환해주고 있다.
👉 외삽(Extrapolation)은 모델이 학습한 범위를 벗어난 입력 데이터에 대해 예측하는 것을 의미한다.
일반적으로 KNN은 입력 데이터의 범위 내에서만 유효하며, 학습된 데이터의 범위를 벗어난 데이터에 대해서는 정확한 예측을 보장하지 않는다.
KNN 알고리즘 주요 하이퍼 파라미터
1. n_neighbors: k의 값(이웃 수) - 새로운 데이터 포인트를 분류할 때 고려할 이웃의 수를 결정.
- k 값이 클수록 모델의 복잡도가 낮아지고, 작을수록 모델의 복잡도가 높아짐
2. weight : 가중치 결정 방법 (uniform - 동일한 가중치, distance - 거리의 반비례 가중치)
3. metrics : 거리측정방식(euclidean, manhanttan)
4. algorithm : 사용할 거리기반 알고리즘 선택
- 'auto' : 자동으로 적절한 알고리즘 선택
- 'ball tree' : 필요한 부분을 빠르게 탐색(공간을 구분하는 데 사용)
- 'kd_tree' : 데이터를 분할하여 차원 축소를 진행
- 'brute' : 완전탐색방식(가장 직관적이지만, 데이터가 크면 비용이 많이 듦)
가중치(weight) 설정에 따른 예측 변화
import numpy as np
import matplotlib.pyplot as plt
from sklearn import neighbors
np.random.seed(0) # 시드 설정
X = np.sort(5 * np.random.rand(40, 1), axis=0) # 0과 5 사이의 균일한 분포에서 40개의 랜덤한 숫자를 생성하고, 그 중 일부를 선택하여 오름차순으로 정렬된 열 벡터 X
T = np.linspace(0, 5, 500)[:, np.newaxis] # 0부터 5까지 500개의 값을 생성하여 500행 1열의 배열 T를 만듭니다.
y = np.sin(X).ravel() # X의 sin을 계산하여 1차원 배열 y로 만듦
# 노이즈 추가
y[::5] += 1 * (0.5 - np.random.rand(8)) # 5의 배수 인덱스 값에 노이즈 추가
n_neighbors = 5
for i, weights in enumerate(["uniform", "distance"]):
knn = neighbors.KNeighborsRegressor(n_neighbors, weights=weights)
y_ = knn.fit(X, y).predict(T)
plt.subplot(2, 1, i + 1)
plt.scatter(X, y, color="darkorange", label="data")
plt.plot(T, y_, color="navy", label="prediction")
plt.axis("tight")
plt.legend()
plt.title("KNeighborsRegressor (k = %i, weights = '%s')" % (n_neighbors, weights))
plt.tight_layout()
plt.show()
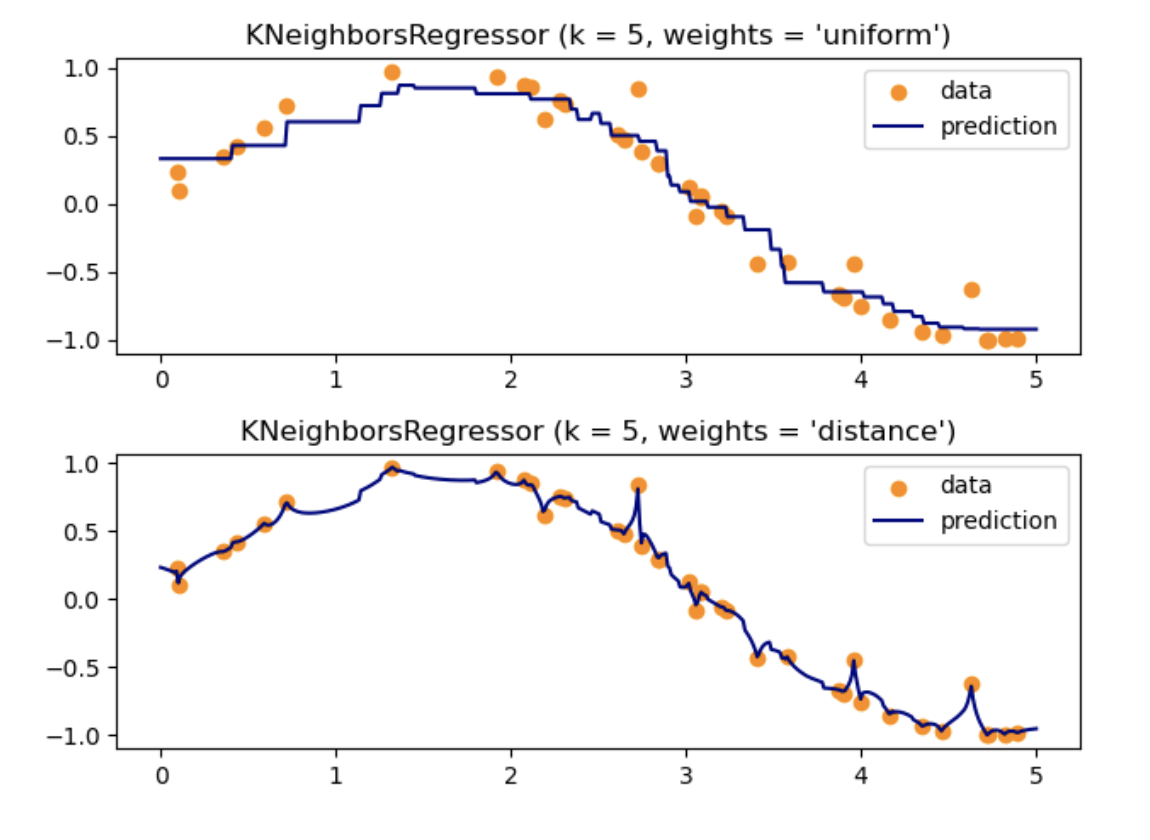
"uniform" : 데이터 포인트에 동일한 가중치를 부여 > 예측값은 각 이웃의 값에 대한 단순한 평균이 된다.
"distance" : 각 이웃 데이터 포인트에 거리에 반비례하는 가중치를 부여 > 따라서 예측값은 더 가까운 이웃에 더 큰 영향을 받게 된다
K 값에 따른 평가지표 변동
캘리포니아 데이터로 교차검증을 통해, k 값에 따라 변화하는 MSE 값을 확인해 보자.
from sklearn.datasets import fetch_california_housing
X,y = fetch_california_housing(return_X_y=True)
# 학습/평가 데이터셋 분리
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=111)
k_values = range(1,20)
mse_scores = []
for k in k_values: # k값
knn = KNeighborsRegressor(n_neighbors=k)
scores = cross_val_score(knn, X_train, y_train, cv=3, scoring='neg_mean_squared_error')
mse_scores.append(-scores.mean())
#MSE 가장 낮은 k 값 찾기
optimal_k = k_values[mse_scores.index(min(mse_scores))]
print(f'Optimal K: {optimal_k}')Optimal K: 9plt.figure(figsize=(15,8))
plt.plot(k_values, mse_scores, marker='o')

👉 K 값이 최적에 수렴한 후, 점차 증가하는 현상을 보인다
🔎 원인 - 과적합 or 과소적합
너무 큰 K값 설정 시 > 과소적합
- 미세한 경계 값을 잘 분류하지 못한다
- 모델이 너무 단순해지고 편향이 높아진다(결정 경계가 더 부드러워짐 > 일반화 능력이 저하 )
너무 작은 K값 설정 시 > 과대적합
- 패턴이 직관적이지 않고, 이상치의 영향을 크게 받는다.
- 모델이 복잡해지고 분산이 높아진다(결정 경계가 더 복잡해짐 > 과적합 가능성 증가 > 일반화 능력 저하)
'Python > Machine Learning' 카테고리의 다른 글
| RFM 기반 군집 분석 (0) | 2024.05.26 |
|---|---|
| K-Means Clustering 알고리즘 (0) | 2024.05.11 |
| [ML]KNN 알고리즘 (2) | 2024.04.07 |
| [ML] 임계값 설정과 평가지표 & ROC 변동 (1) | 2024.03.30 |
| [ML] 머신러닝 평가지표 - 회귀 모델 MSE, RMSE, MAE (0) | 2023.09.16 |



